Научный форум dxdy
Регистрация Вход. Ответы Mail. Вопросы - лидеры. Требуются ли деньги на борьбу с научными открытиями, когда народу есть нечего априори? Лидеры категории Лена-пена Искусственный Интеллект.












Ост а точный чл е н приближённой формулы, разность между точным и приближённым значениями представляемого этой формулой выражения. В зависимости от характера приближённой формулы О. Обычно задача исследования О. Например, приближённой формуле.







| 49 | Последний раз редактировалось yoloven | |
| 114 | Регистрация Вход. Ольга Александровна, помогите решить! | |
| 322 | Конев В. | |
| 207 | Пусть функция f x определена в некоторой окрестности точки x0 и n раз дифференцируема в точке x0. | |
| 124 | Формула называется формулой Тейлора с центром в точке a; - остаточный член в формуле Тейлора в общем виде. Рассмотрим вспомогательную функцию. | |
| 195 | Конев В. |
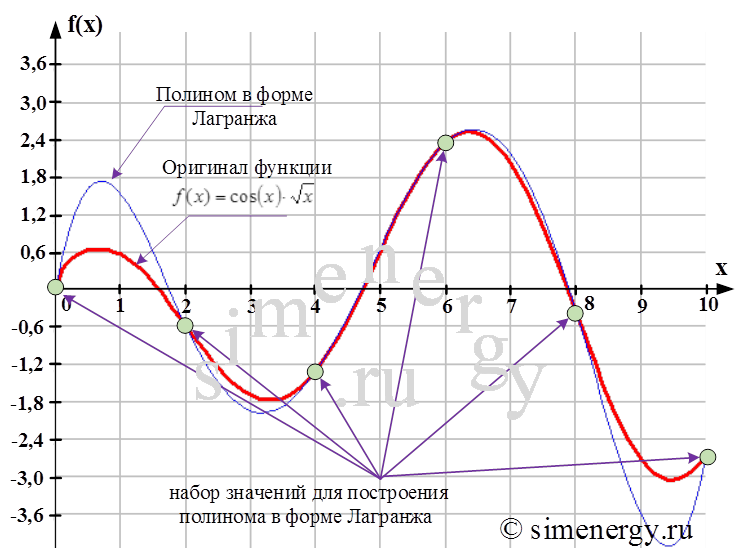
Частный случай разложения в ряд Тейлора в нулевой точке называется рядом Маклорена. Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка. Обобщением понятия ряда Тейлора в функциональном анализе является ряд Фантапье. Функция называется аналитической на промежутке на множестве , если она является аналитической в каждой точке этого промежутка множества. Ответ: нет.





