Построить натуральную величину сечения поверхности плоскостью

Определение взаимного положения плоскости и поверхности — задача позиционная, для решения которой применяется метод вспомогательных секущих плоскостей. В качестве вспомогательных секущих плоскостей используются проецирующие плоскости — плоскости перпендикулярные плоскостям проекций, поэтому основу метода вспомогательных секущих плоскостей составляет алгоритм решения задачи по нахождению проекций линии пересечения поверхности с проецирующей плоскостью. В этом случае нужно выполнить анализ положений поверхности и плоскости относительно плоскостей проекций.

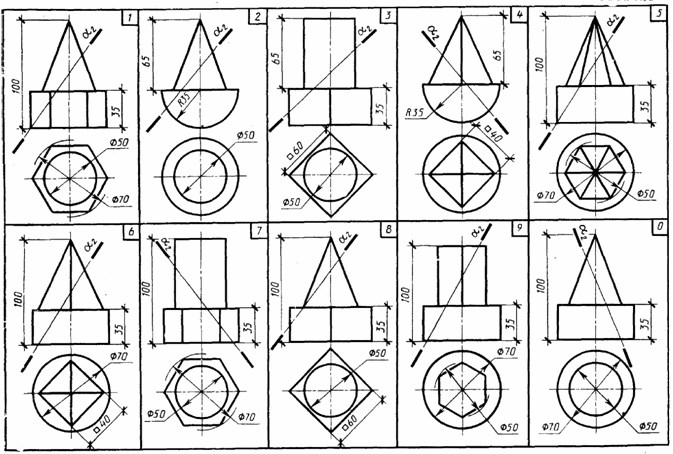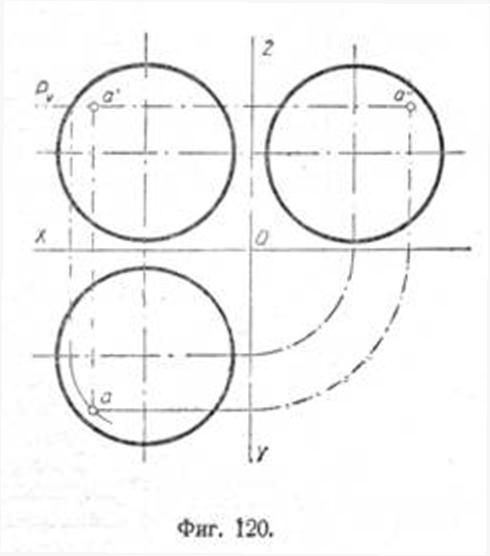
Сечение поверхности конуса плоскостью общего положения

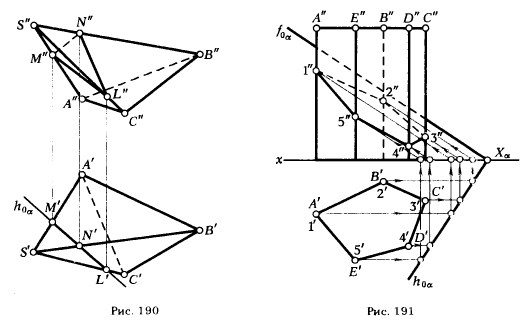
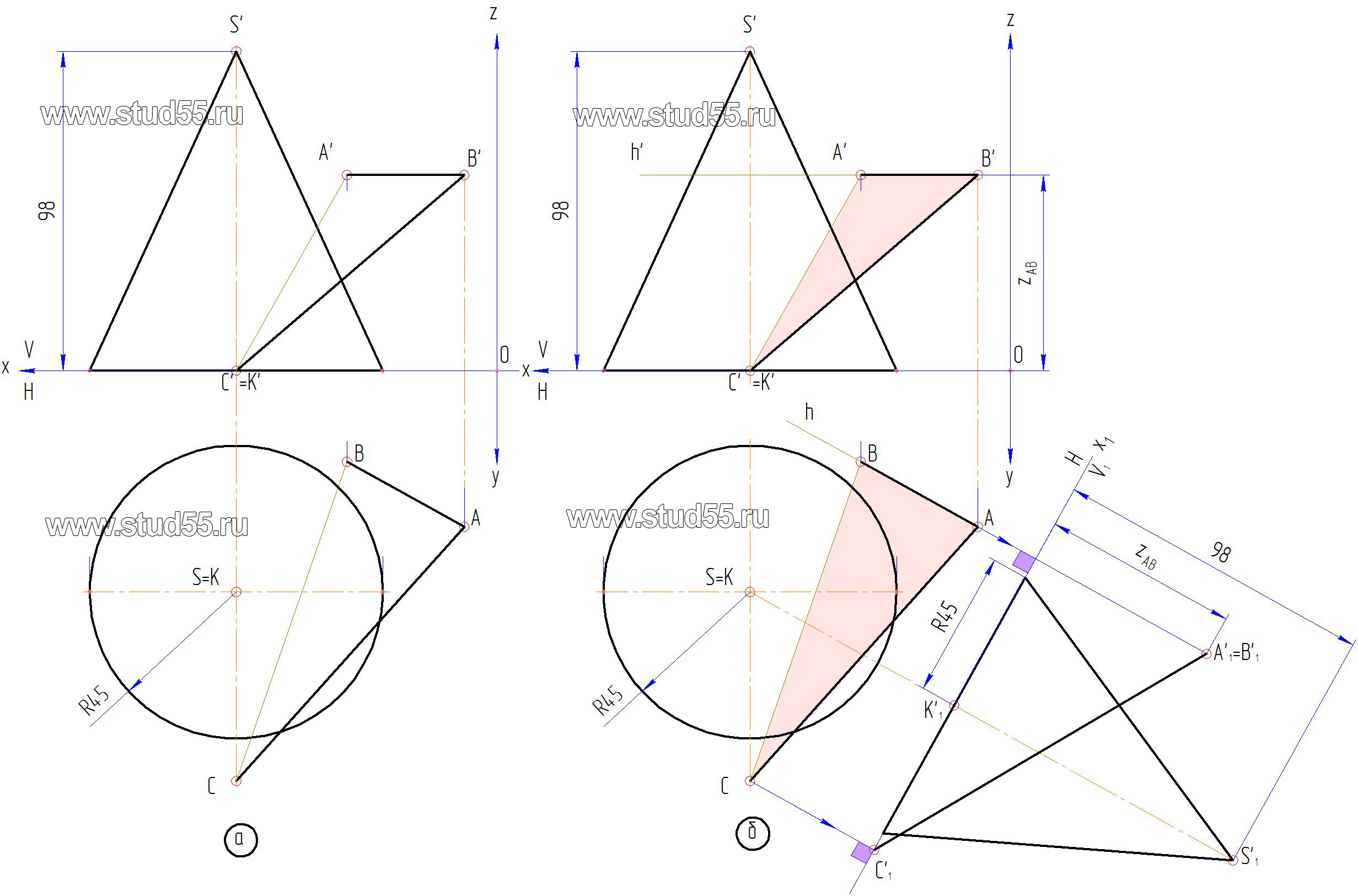
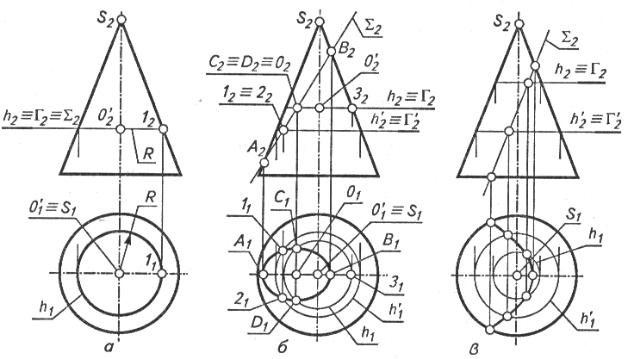
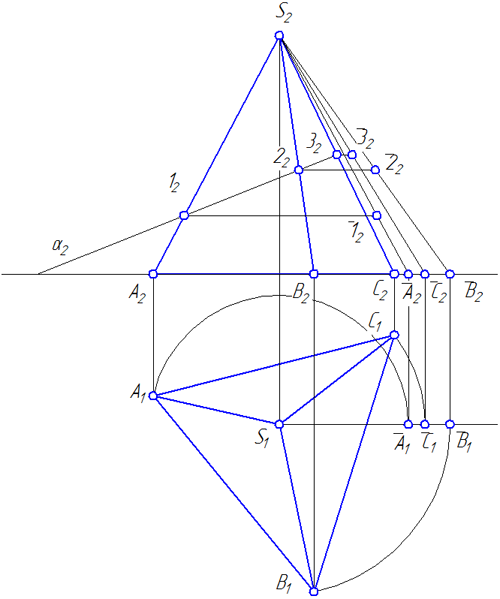
При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности. Начальные данные представлены на рисунке ниже. Построение линии пересечения следует начинать с нахождения её характерных точек. Они определяют границы сечения и его видимость по отношению к наблюдателю.

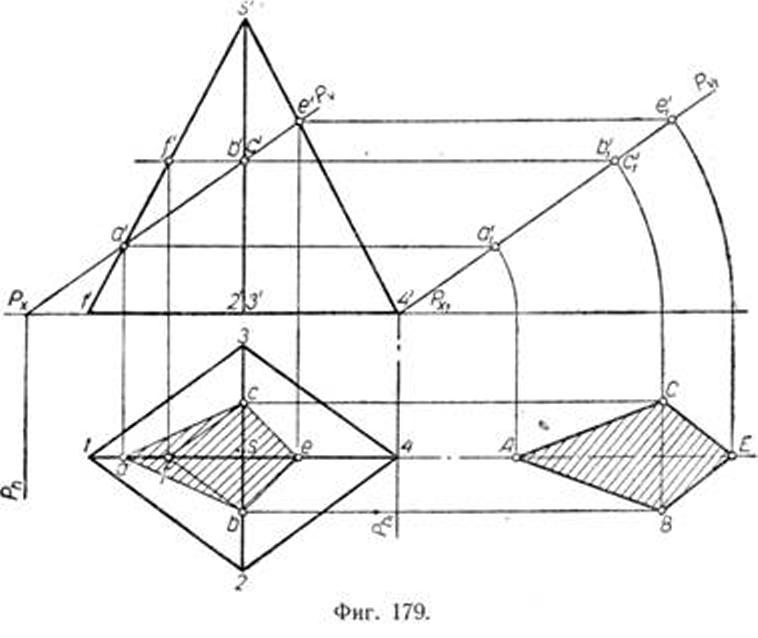
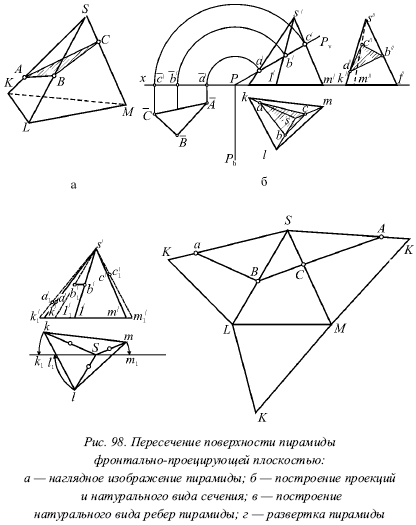
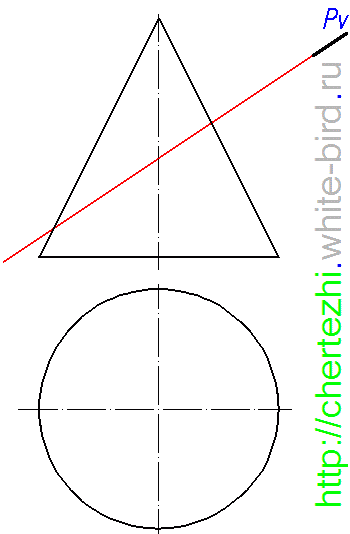
Построить линию пересечения поверхности проецирующей плоскостью. Найти истинную величину сечения. Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь.

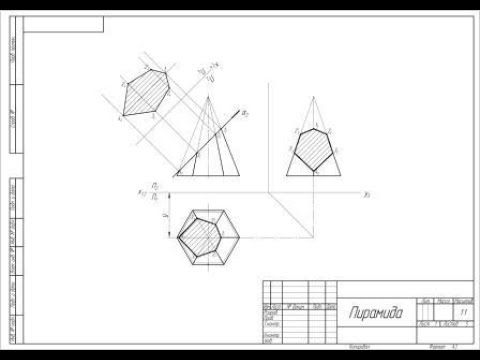
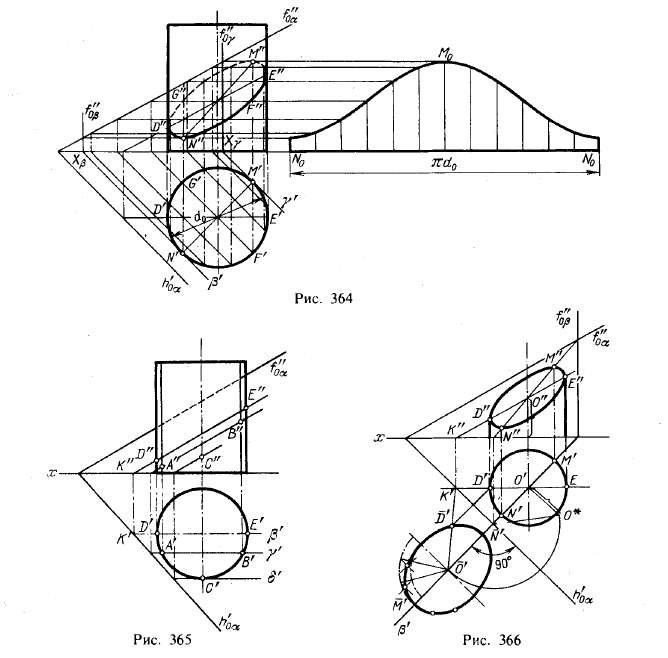
• Построение сечения цилиндра. Построение сечения конуса.
• Для построения линия пересечения двух плоскостей, которая является прямой линией, необходимо определить две точки М М 1 , M 2 и N N 1 , N 2 , общие для заданных плоскостей.
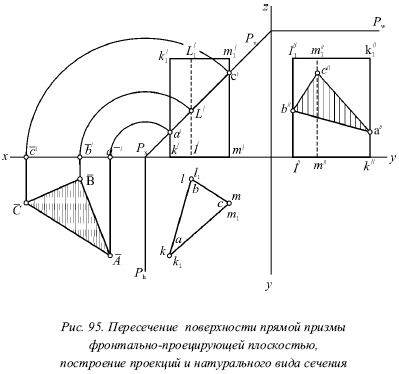
• Построение сечения призмы плоскостью частного положения.
• Если одна из пересекающихся поверхностей - плоскость, то такое пересечение принято называть сечением поверхности плоскостью. Полученную при этом линию называют линией сечения.

Похожие статьи

• Молодая девушка с натуральной грудью
• Услуги по монтажу панно и мозаики из натурального камня
• Пошив сумок из натуральной кожи в г кирове
• Доли рынка натуральной косметики в украине